© 2006 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).
Printed from https://www.damninteresting.com/curio/rapatronic-nuclear-photographs/
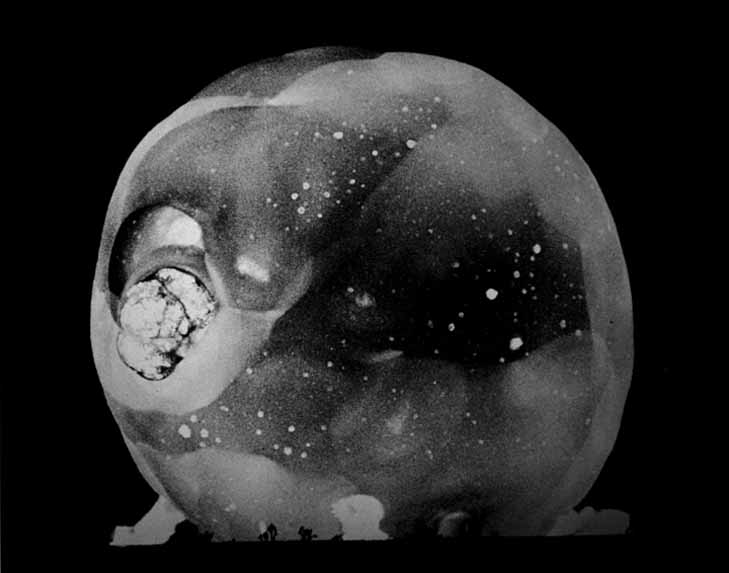
During the early days of atomic bomb experiments in the 1940s, nuclear weapons scientists had some difficulty studying the growth of nuclear fireballs in test detonations. These fireballs expanded so rapidly that even the best cameras of that time were unable to capture anything more than a blurry, over-exposed frame for the first several seconds of the explosion.
Before long a professor of electrical engineering from MIT named Harold Eugene “Doc” Edgerton invented the rapatronic camera, a device capable of capturing images from the fleeting instant directly following a nuclear explosion. These single-use cameras were able to snap a photo one ten-millionth of a second after detonation from about seven miles away, with an exposure time of as little as ten nanoseconds. At that instant, a typical fireball had already reached about 100 feet in diameter, with temperatures three times hotter than the surface of the sun.
Edgerton was a pioneer in high-speed photography, receiving a bronze medal from the Royal Photographic Society in 1934 for his work in strobe photography. He used the technique to photograph many events that typical cameras were much too slow to capture, such as the instant of a balloon bursting, and bullets impacting various materials. He developed the rapatronic camera about ten years later, for the specific purpose of photographing nuclear explosions for the government.

In a typical setup at a nuclear test site, a series of ten or so rapatronic cameras were necessary, because each was able to take only one photograph—no mechanical film advance system was anywhere near fast enough to allow for a second photo. Another mechanical limitation which had to be overcome was the shutter mechanism. Mechanical shutters were incapable of moving quickly enough to capture the instant one ten-millionth of a second after detonation, so Edgerton’s ingenious cameras used a unique non-mechanical shutter which utilized the polarization of light.
As you’ve probably noticed, if one takes two pieces of polarized glass (such as the lenses from polarized sunglasses) and lays them atop one another at 90° angles, no light is able to pass through. This is because each one filters out light which is not polarized to its polarization axis, so the combination of the two lenses filters out 100% of the light. Edgerton ‘s rapatronic camera used this property in combination with a Kerr cell—a nifty and obscure optical element which rotates light’s plane of polarization when a high-voltage field is applied.
The rapatronic camera lens included two perpendicular polarizers, which prevented any light from entering—but sandwiched in between them was a Kerr cell. When the Kerr cell was energized, it affected all of the light which passed through the first polarizer by rotating its plane of polarization by 90°, realigning the light to match the second polarizer. This allowed the light to pass through both polarizers whenever the Kerr cell was provided with electricity, which is exactly what was done for 10 nanoseconds at the critical moment. This assembly provided an extremely fast non-mechanical shutter, exposing the film to the light for a minuscule fraction of time.

The resulting extraordinary photographs revealed intricate details of the first instant of an atomic explosion, including a few surprises such as irregular “mottling” caused primarily by variations in the density of the bomb’s casing. It also showed the detail of the “rope trick effect,” where the rapid vaporization of support cables caused curious lines to emanate from the bottom of an explosion. But even aside from the scientific utility of the images, they certainly show that these fantastically destructive nuclear fireballs have a hauntingly beautiful side, even if it only lasts for one ten-millionth of a second.
© 2006 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).
Printed from https://www.damninteresting.com/curio/rapatronic-nuclear-photographs/
Since you enjoyed our work enough to print it out, and read it clear to the end, would you consider donating a few dollars at https://www.damninteresting.com/donate ?
Is it right that when one sets 2 polarization filters aligned 90 degrees one from each other they prevent light from passing though? My understanding is that 25% of the light would remain after the second filter, as quantum physics mandate. Actually, the fact that a polarization filter, which only allows light to pass coming from a single polarization angle, allows 50% of the light to pass through is something puzzling (just consider that light is supposed to have a full 360 degrees polarization distribution), and can only be undersood under the light of quantum mechanics (no pun intended).
cool
Well, I’m sure orthogonal polarization blocks all light, because I’ve played around with polarized screens. I think the polarization can be expressed as an angle to a plane, so polarizing filters that are parallel to each other, but rotated 90º, are both measuring the same quantum characteristic, not two complementary ones. I’m going to check this out in a sec:
http://en.wikipedia.org/wiki/Polarization
The explosions almost look like upclose photos of germs and other bacteria I’ve seen.
wow didn’t realize they were 3times as hot as the sun…question though. how far is the sun from us and how hot is it? i mean with it so far away it’s already burning hot on a sunny day, if the bombs are so hot wouldn’t they pretty much destroy the earth badly? and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?
I found one quote that said the camera was used 7 miles away with a 10 foot lens, so the cameras didn’t have to (and couldn’t) survive the temperature of the sun.
superdude882 said: “and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?”
What do you think caused the “rope trick effect”?
I can remember having practice drills in grade school when we would all file out of the classroom into the hallway, sit down on the floor facing the lockers and put our coat or jacket over our heads. I guess this kinda of shoots this civil defense plan of nuclear survival to heck. Or better yet the old saying in the 60’s on how to survive a nuclear blast was to sit down when you saw the bright flash of light, put your head between your legs and kiss your butt goodbye. We lived near the tank plant in Warren, Michigan and we would not have known what hit us since it being the only tank plant in the country at the time. We would have been the first to be vaporized.
wileybot said: “What do you think caused the “rope trick effect”?”
Doh- gotta love wikipedia
Anonymous User said: “Is it right that when one sets 2 polarization filters aligned 90 degrees one from each other they prevent light from passing though? My understanding is that 25% of the light would remain after the second filter, as quantum physics mandate. Actually, the fact that a polarization filter, which only allows light to pass coming from a single polarization angle, allows 50% of the light to pass through is something puzzling (just consider that light is supposed to have a full 360 degrees polarization distribution), and can only be undersood under the light of quantum mechanics (no pun intended).”
I can’t expertly speak on quantum physics, but I do know my basic optics principles. I’ll use a clock to make it simpler to explain.
The clock represents the cross-section of a ray of light with a full 360 degrees of polarization after it has passed though a horizontally polarized filter. 100% of the light waves aligned with the 12 & 6 o’clock positions will be eliminated. 66 2/3% of the waves aligned with the 1 & 7 and 11 & 5 o’clock positions will be eliminated. 33 1/3% at the 2 & 8 and 10 & 4 o’clock positions and 0% at the 3 & 9 o’clock positions.
Now put a vertically polarized filter in front of what remains of the ray of light. 100% of the waves at the 3 & 9 o’clock positions are eliminated, 66 2/3% at the 2 & 8 and 10 & 4, etc. So after the ray has encountered both filters, 100% of the light waves have been eliminated at each position.
I hope that clears it up a little for you Anonymous :)
superdude882 said: “wow didn’t realize they were 3times as hot as the sun…question though. how far is the sun from us and how hot is it? i mean with it so far away it’s already burning hot on a sunny day, if the bombs are so hot wouldn’t they pretty much destroy the earth badly? and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?”
Nah, if I recall right, the surface of the sun isn’t all that hot, only around 5,500 K (about 5,227 C), Its the core and the Corona that you would want to worry about. In fact, I recall that lighting is has a temp of about 5 times hotter then the surface of the sun.
Also, there is a difference between getting hit with 15000 K of heat (transfered via air/shockwaves) and getting hit with 5000 K of heat transfered via plasma/super heated gas. Just a thought though.
Anybody correct me if I’m wrong though, memory is always what its cracked up to be.
Fantastic photos (i checked the first link). Who would have ever thought that doom could be so beautiful?
superdude882 said: “wow didn’t realize they were 3times as hot as the sun…question though. how far is the sun from us and how hot is it? i mean with it so far away it’s already burning hot on a sunny day, if the bombs are so hot wouldn’t they pretty much destroy the earth badly? and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?”
Nah, if I recall right, the surface of the sun isn’t all that hot, only around 5,500 K (about 5,227 C), Its the core and the Corona that you would want to worry about. In fact, I recall that lighting is has a temp of about 5 times hotter then the surface of the sun.
Also, there is a difference between getting hit with 15000 K of heat (transfered via air/shockwaves) and getting hit with 5000 K of heat transfered via plasma/super heated gas. Just a thought though.
Anybody correct me if I’m wrong though, memory is always what its cracked up to be.
I don’t have any hard data to back this up, but I would also imagine that it depends on time exposed as well. The sun-like temps at the time of detonation quickly dissipate as the fireball expands since the heat source disappears remarkably quickly. The sun, on the other hand, has been pumping out its life-giving solar goodness for billions of years.
superdude882 said: “wow didn’t realize they were 3times as hot as the sun…question though. how far is the sun from us and how hot is it? i mean with it so far away it’s already burning hot on a sunny day, if the bombs are so hot wouldn’t they pretty much destroy the earth badly? and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?”
The article says that the nuclear bomb has a heat 3times that of the surface of the sun (so about 16,500K) but the core temperature of the sun is about 13.6 MK (over 800times hotter than an exploding A-bomb). And as already stated the suns energy output is continuous as opposed to a nuclear bomb where the energy is released in a very short time period only. So thats why nukes don’t destroy the Earth totally they just make a really big mess of it for political reasons.
Does it really matter how hot it is? …or how many more times hotter than the sun, or whatever?
Anything over a 100 degrees is still going to burn. Besides, they don’t make anti-sun or anti-A bomb burn cream.
Anonymous User said: “. . . Actually, the fact that a polarization filter, which only allows light to pass coming from a single polarization angle, allows 50% of the light to pass through is something puzzling (just consider that light is supposed to have a full 360 degrees polarization distribution), and can only be undersood under the light of quantum mechanics (no pun intended).”
The misunderstanding here is that you forget that electromagnetic polarization is a vector, and can be broken into orthoganal vector components that add up to the original vector.
That means if you have light that is not perfectly aligned with a particular polarization, only cos θ * the amplitude of the light will get through, where θ is the angle between the polarization of the light and the polarization of the filter.
This means that even if the light is 89° off, a tiny bit of light will still get through because cos 89° > 0. However, if the light is exactly 90° off, no light will make it through at all because cos 90° is exactly 0.
. . . and if the light is perfectly aligned, all of it should get through except for the loss incurred by going through the medium of the filter, since when it is aligned, θ = 0, and cos 0° is exactly 1, or 100%.
. . . by the way, notice that I didn’t need to understand any quantum mechanics to explain that. There is a lot of quantum mechanics involved in the study of polarization effects when you are dealing with individual photons, but polarization is easier than that and easily tractable for the most part if you approach it as a bunch of vectors to be dealt with using trigonometry and the pythagorian theorem.
wileybot said: “What do you think caused the “rope trick effect”?”
Wikipedia’s article on this says that the “rope tricks” are caused by the cables or ropes absorbing the intense light and spontaneously vaporizing because of it. Experiments done on the cables showed that the cables painted black exhibited the strongest “rope trick” effect, whereas the cables wrapped in aluminum foil or reflective paint showed no rope trick effect at all.
Here’s the link: http://en.wikipedia.org/wiki/Rope_trick_effect
A wee bit more on vectors and polarization:
If you want exactly half the light to get through, the polarizing filters should be 60° to each other, not 45° as one might intuitively suspect:
cos 60° is exactly 0.5.
cos 45° is about 0.707 (half the square root of two), which is larger than 0.5.
Ah. . . I can’t resist posting a wee bit more.
If you have two polarizers that are polarized 90° to each other, no light makes it through the two filters. However, if you stick another filter between them that is 45° off, you’ll notice that about half light comes through simply after the insertion of the filter that is 45° off.
This may seem mysterious, but once you understand polarizations as a vectors, it all makes sense. Filters that are rotated by 90° let no light through because no vector has components that are orthoganal to itself. (That’s a fancy way of describing the phenomenon that a vertical pin casts no shado when lit straight from above.) By inserting a polarizing filter that is 45° off, about 70.7% of the light makes it through, polarized now to 45°. The next filter, which was 90° off from the first let no light through coming straight through from the first filter, but, being only 45° off from the inserted filter, it lets through ~70.7% of the light coming through the inserted filter. Each 45° offset lets through half the square root of two. Square that value, and you get ½. That’s why two filters rotated 90° lets no light through, whereas the insertion of a filter at 45° between the two mysteriously lets light through.
Whoa, I just stumbled upon an article on this on Wikiepedia recently… sounds like a case of that “Baader-Meinhof Phenomenon” the other article talked about. Interesting stuff anyway, especially the ‘rope trick.’
Everything about how hot a bomb is vs. the sun
Warning: This oversimplifies things quite a bit, and some of my terminology may not be 100% correct… please correct me :-)
Keep in mind that there’s a huge difference between heat (energy) and temperature (a measure of how quickly molecules are shaking around). The reason that a one of these bombs doesn’t destroy the planet, even though it’s “hotter” than the sun, is because the bomb isn’t putting out nearly as much energy.
In my fairly limited exposure to physics, I learned about the Stefan-Boltzmann law, which describes how much energy is radiated from a surface – it is a function of temperature and area. Despite the greater temperature, the “area” of that heat is significantly smaller than the surface of the sun… and therefore the amount of energy coming out is less.
dwhitter said: “We lived near the tank plant in Warren, Michigan and we would not have known what hit us since it being the only tank plant in the country at the time. We would have been the first to be vaporized.”
Perhaps, but from some maps I’ve seen showing where we expected a nuclear attack to be targeted, you might be OK. Tanks are one thing, but in a preemptive nuclear attack, the main targets are our land-based nuclear missile silos. While tanks might be useful in the ensuing ground war, it’s a far better tactic to try an take out every possible counter-missile right off the bat. I’ll see if I can’t find a link to those images, they’re laid out by state. Some of the midwest and north-midwest are solid yellow with blast zones. I figure it must take a hell of a pummeling to take out an underground nuclear silo….
I agree with white_matter on the resemblance to bacteria. Those explosions are eerily beautiful. They also vaguely remind me of those images of water droplets hitting water taken with very high speed cameras. Strangely symmetrical and organic…
The article said: These single-use cameras were able to snap a photo one ten-millionth of a second after detonation from about seven miles away, with an exposure time of as little as ten nanoseconds. At that instant, a typical fireball had already reached about 100 feet in diameter
The numbers here don’t add up. According to Google (http://www.google.com/search?q=1+lightsecond+%2F+10000000+in+feet), 1 10 millionth of a lightsecond is about 100 feet. I can see how the fireball may have expanded to almost 100 feet as matter approaches the speed of light, but how could the resulting image reach the camera 7 miles away? That should take about 37 microseconds, or 370 “10 millionths” of a second.
But still, the pictures are pretty.
everything is delayed by 37 microseconds, assuming the timer would detonate the bomb instantly the light of the moment of detonation reaches the camera 37 microseconds later and the blast reaches 100 feet .1 microsecondes later or 37.1 microsecondes from the point of detonation. The cameras timer most probably was calibrated to account for the light-speed delay, otherwise they would have taken photos of 37 us before the detonation.
I had the pleasure of working with Edgerton on a project with the U.S.Postal Dept. “Doc” was a real wizard at what he did, and his intrest and insight was an inspiration to all of us on the project. He should be refered to as “The father of high speed photography” Lukens
WOW. Those pictures are soooo cool.
A couple of things:
No matter has to move 100 feet for the size of the blast to reach 100 feet. A lot of the energy is transferred by electromagnetic radiation (with a HUGE range of frequencies), which moves at the speed of light. Be careful not to confuse the wave speed with the particle speed.
Also, about the polarization: Nobody seems to be noticing the difference between amplitude and intensity. But the latter (intensity, energy per area per time) is proportional to the square of the former (amplitude, peak electric field magnitude). Everyone seems to be calculating amplitudes, and then saying that that’s the fraction of the light that gets through. That may be the fraction of the electric field, but the fraction of the energy (the same as the fraction of the photons, and usually taken to be the more meaningful quantity) is the square of that. So if the stack of polarizers transmits, say, 70.7% of the amplitude, then half the light energy is getting through.
A polarizer in effect eliminates all of the electric field in one direction but has no effect on the electric field in the other direction (perpendicular to the first direction). With this fact, the cosine function, and knowing that energy is proportional to electric field squared, you can solve all of these problems. A fun exercise is to see how high the transmittance can get if you can insert a very large number of polarizers in between the crossed polarizers.
Describing the same event in terms of photons is a little more complicated but gives the same answer in the end. Part of the problem is that there’s more than one “consistent history,” i.e. more than one logically and mathematically correct series of classical-like events that could be chosen to describe the quantum mechanical process, and the various histories are mutually inconsistent. What’s the difference between a set of photons that are all randomly polarized and a set of photons that are all either x or y polarized, with 50% probability of each, and no correlations? If I’m not mistaken, they have the same density operator, so there is in principle no way to distinguish them.
I’m sure everyone has seen Edgerton’s famous photographs of a milk drop and a bullet piercing an apple or balloon. But this is something else. Too bad we couldn’t see these images through a rapatronic video camera. Also, to jfl2: I’m curious how high-speed photography was used in a project for the postal service. There doesn’t seem to be an obvious connection there.
sh0cktopus said: “I’m curious how high-speed photography was used in a project for the postal service. There doesn’t seem to be an obvious connection there.”
This is just a guess, but it could be related to the optical scanners that were developed for mail sorting. Not quite the same as photography, but to get an image sharp enough to be analyzed by OCR software from an envelope zipping through a slot probably requires a lot of the same kind of expertise.
Berkana said: “. . . by the way, notice that I didn’t need to understand any quantum mechanics to explain that. There is a lot of quantum mechanics involved in the study of polarization effects when you are dealing with individual photons, but polarization is easier than that and easily tractable for the most part if you approach it as a bunch of vectors to be dealt with using trigonometry and the pythagorian theorem.”
Ha! Nice Berkana. Einstein once said that if you couldn’t explain something to a six year old then you don’t truly understand it yourself. That quote was paraphrased but it gets the point across. I’m looking forward to taking some modern physics myself. It’ll be fun. Like pie. Alan should get some too. Nothing relieves the stress of a busy schedual like a nice big slice of pumpking pie with double scooped whip cream. mhmm.
superdude882 said: “wow didn’t realize they were 3times as hot as the sun…question though. how far is the sun from us and how hot is it? i mean with it so far away it’s already burning hot on a sunny day, if the bombs are so hot wouldn’t they pretty much destroy the earth badly? and the cameras would be able to survive on the sun then? since they can withstand something hotter than 3 suns it should be able to take on one?”
Admiral Dread did a good job providing the temperature you were asking about, so I’ll pick up some of the other stuff. The sun is, on average, about 98,000,000 miles from the Earth. The reason a nuke doesn’t destroy the Earth with the temperatures generated is that the amount of energy released in total is inconsequential compared to that of the Sun, and is a very localized event. The Sun’s diameter is roughly 870,000 miles while the Earth has a diameter of a little under 8,000 miles. So the 2-dimensional area of the photosphere of the sun facing the Earth is roughly 594,166,500,000 square miles – radiating heat at about 5,800K over that entire surface (and the corona of the Sun has temperatures reaching at times up to a million K… and since the corona of the sun is outside of the photosphere, it has an even larger surface area).
The size of the fireball from a nuke is incredibly smaller than that (if it were a 20 mile diameter fireball, the 2D surface area would be 314 miles, or nine decimal places smaller than the Sun and divided by a constant) and maintains that temperature for a very short time. If it were somehow able to maintain that temperature for an extended amount of time, trouble could very well ensue. You can pass your hand through a flame, but the short duration keeps you from getting a burn. Keep your hand there for a minute…. you get the picture.
I love having the chance to speculate before bothering to learn why it’s wrong…
I’d never heard of the Kerr Effect, but a rotation of 90 degs is mentioned for these cameras. Given the intensity of light from a bomb blast, it seems one would only need rotate the polarizati0n the tiniest bit.
I’m still puzzled by something in the picture, and I’ve seen it before in photos of nuclear explosions. In bottom righthand quadrant of the picture there are about 5 sort of vertical lines. Now, if I’m understanding the rope trick effect properly, those are the spike-like protrusions on the fireball. So what are these lines we’re seeing? Anybody have an explanation?
lol them 3 little lines in the lower right hand corner sorry im at fault i was trying to jump start my space ship where was the engerizer bunny when i needed him??
ps dont mind me just a freak of nature any way but the pic’s are pritty cool!
gypse.
gypse: I think they used to launch rockets to leave smoke trails in the air before detonating the A-bomb,
the smoke trails would show the effect of the shockwave in the air.
The “rope trick effect”, as I recall, is the wires fluorescing (essentially turning into plasma) from the gamma (or was it X-ray?) burst, which precedes the visual effects by a few picoseconds (or is it femtoseconds?). I’m sure it’s on wikipedia…
Ehh, just read it, apparently it’s thermal shock.
Maybe is had to do with the film speed. It could be that 25% of light would not even expose the film. After all we are looking at something that’s as bright or brighter than the sun. It could be that it takes 100% to create a proper exposure. Then again there could be an exposure from 25%, but its washed out from the full exposure.
OK on the rope trick phenomonon – but what about the small bright spots than some fireballs show? Are they from birds in the air, caught in the explosion – or what?
If the lines of polarization were less than the amplitude of the light would light get through spread out showing the quantum wave function? So if you put those together at 90° to each other could light still get through
It would be neat to see those pictures in ultraviolet, infrared, gamma, microwave, et. al. Wavelengths only. I suppose a polarized filter wouldn’t work for gamma and x ray pictures even if the polarization lines were made of lead I assume they’d be to thin to filter anything. It would require an entirely different Camara design. It would be cool to see pics of other Wavelengths than just visible though.
To the anonymous user in the first cmoment.
The way a polarising filter works is by only allowing light through traveling in one vectors direction.
Take the example of a vertical filter. Only light oscillating in the vertical direction can pass through. Now imagine the second filter aligned in the same direction. All the light goes through as it is all oscillating in the same direction.
If you tilt the second filter by one degree you block out some of the light but not all of it. I can’t explain it very well but once the second filter has been rotated 90 degrees none of the light can pass through because none of it is oscillating in that direction.
I think it’s schnells law that describes this but I can’t remember
I don’t know if somebody already mentioned this, but according to Wikipedia (and I don’t know how accurate that is), the author of the Trinity photo on top is not Edgerton, but Berlyn Brixner.
https://en.wikipedia.org/wiki/File:Trinity_Test_Fireball_16ms.jpg
@Joe: Oops, you are correct. I updated the image a few weeks ago and mistakenly used a non-rapatronic photo. Thanks for the heads up!
An engineer’s brain is a freak of nature.